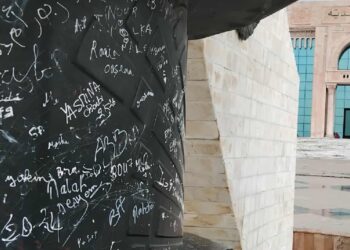ACTUALITÉ NATIONALE
Tunisie : Appel à la vigilance sur les routes face aux pluies attendues
L’Observatoire national de la sécurité routière a appelé l’ensemble des conducteurs et usagers de la route à faire preuve d’une...
Lire la suiteCrise au Moyen-Orient : Tunis prépare des scénarios d’évacuation pour ses ressortissants
La Tunisie prépare des scénarios d’évacuation d’urgence pour ses ressortissants dans certains pays du Golfe, en fonction de l’évolution de...
Lire la suiteTunisie : 153 millions de dinars pour moderniser les lignes de chemin de fer du phosphate
La commission des finances et du budget a entendu, lundi 9 mars 2026, le ministre du Transport et son équipe...
Lire la suiteTunisie : 17 millions de dinars pour réparer le littoral
Le ministre de l’Environnement, Habib Abid, a annoncé un premier bilan des dégâts subis par le littoral tunisien dans plusieurs...
Lire la suiteINTERNATIONAL
SPORT
CULTURE
CHRONIQUES
Découvertes : Les trois plus anciennes médersas de Tunis
Les médersas de Tunis sont des anciens foyers d'étudiants de l'université de la Zitouna. Nombreuses, ces institutions se trouvent éparpillées...
Lire la suiteSnapshot : Graffitis sur le monument de la Kasbah
Situé entre l'hôtel de ville, plusieurs ministères et le collège Sadiki, le monument national de la Kasbah se trouve au...
Lire la suiteRamadan : Quand les restaurants font le plein pour l’Iftar
Il y a quelques décennies, dîner au restaurant durant le mois de Ramadan rimait avec célibat ou famille éloignée. De...
Lire la suiteTENDANCES
Orange Fab Tunisie lance sa 8ᵉ cohorte 100% IA pour accélérer les start-up innovantes
Orange Fab Tunisie, l’accélérateur corporate d’Orange Tunisie, ouvre sa 8ᵉ cohorte avec une édition entièrement dédiée à l’intelligence artificielle. Depuis...
Lire la suite